使用
Proof of Lagrange Multipliers 证明正文
copyright :MIT OpenCourseWare
用于个人学习,本网站进行了翻译
本网站附载了该PDF 点击打开
Here we will give two arguments, one geometric and one analytic for why Lagrange multipliers work.
这里我们给出 几何式的和分析式的两种证明方式来说明为什么 拉格朗日乘数法起作用。
临界点:Critical points --“等价证明”条件
--∇ 是梯度算子(在空间各方向上的全微分)
For the function w = f(x, y, z) constrained by g(x, y, z) = c (c a constant) the critical points are defined as those points, which satisfy the constraint and where ∇f is parallel to ∇g. In equations:
对于(目标函数)方程w = f(x, y, z) 在条件约束g(x, y, z) = c(c是常量)的问题,临界点是 满足 “∇f 平行于 ∇g” 的. 等式如下:
∇f(x,y,z)=λ∇g(x,y,z) and g(x,y,z)=c.
声明:Statement of Lagrange multipliers
For the constrained system local maxima and minima (collectively extrema) occur at the critical points.
在受约束系统中,局部最大值和最小值(统称为极值)出现在临界点处.
1.几何法
(We only consider the two dimensional case, w = f(x, y) with constraint g(x, y) = c.) For concreteness, we’ve drawn the constraint curve, g(x, y) = c, as a circle and some level curves for w = f(x, y) = c with explicit (made up) values. Geometrically, we are looking for the point on the circle where w takes its maximum or minimum values.
(我们仅考虑两维的情形,目标函数为w = f(x, y)且约束条件为g(x, y) = c)为了具体说明,我们画出了约束曲线g(x, y) = c其是一个圆,此外, 目标函数w = f(x, y) = c是一些 有着明确值 的 水平曲线(level curves). 几何上讲,我们寻找 使得函数w达到其极值时,那时圆上的点的坐标
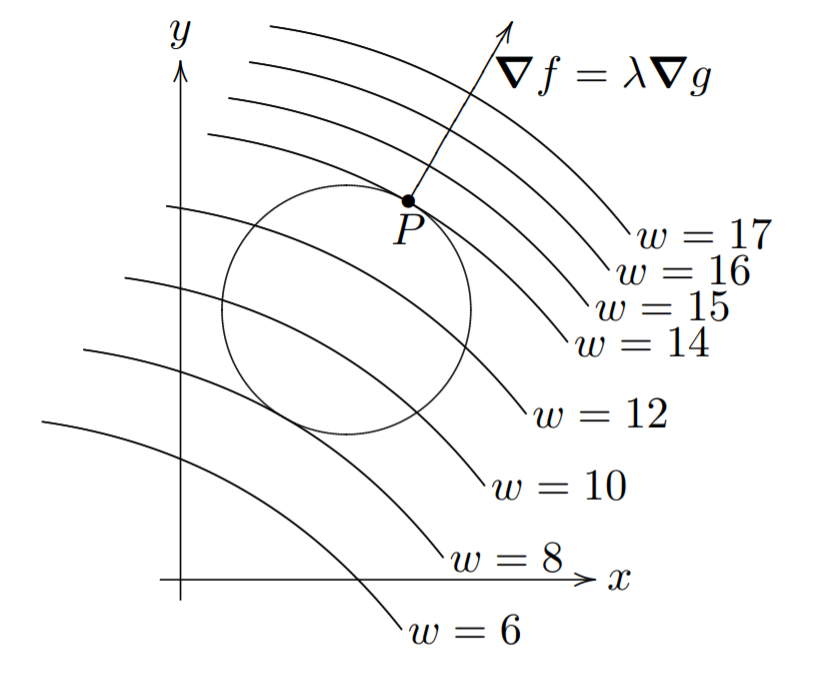
Now, start at the level curve with w = 17, which has no points on the circle. So, clearly, the maximum value of w on the constraint circle is less than 17. Move down the level curves until they first touch the circle when w = 14. Call the point where the first touch P. It is clear that P gives a local maximum for w on g = c, because if you move away from P in either direction on the circle you’ll be on a level curve with a smaller value.
现在,从w=17的水平曲线开始,可见其没有在圆上的点.所以,显然在约束圆下目标函数w的极大值小于17 向下移动水平曲线直至w=14,其首次接触到约束圆,记此点为P。由图可见,P点是在约束g(x,y)=c(圆)下,目标函数w取到极大值的极大值点。(倘若满足约束的目标函数点在约束圆上由P点在任一方向移动只会得到更小的目标函数值).
Since the circle is a level curve for g, we know ∇g is perpendicular to it. We also know ∇f is perpendicular to the level curve w = 14, since the curves themselves are tangent, these two gradients must be parallel.
由于圆是g(x,y)=c的水平曲线,我们可知∇g是垂直于g(x,y)的。 又因为 ∇f是垂直于w(x,y)=14, 两曲线相切于P点,故在P点处 ∇f // ∇g. (个人理解,如果从图上说上讨论问题,应说明P点)
Likewise, if you keep moving down the level curves, the last one to touch the circle will give a local minimum and the same argument will apply.
同理,如果你向下移动(目标函数)水平曲线w(x,y),最后的相切于圆的点将给出目标函数的极小值
2.分析法 (三维角度下)
Suppose f has a local maximum at P on the constraint surface. Let r(t) = (x(t), y(t), z(t)) be an arbitrary parametrized curve which lies on the constraint surface and has (x(0), y(0), z(0)) = P. Finally, let h(t) = f(x(t), y(t), z(t)). The setup guarantees that h(t) has a maximum at t = 0.
设f在在约束条件下于P点处取得局部最大值(极大值) 令r(t) = (x(t), y(t), z(t)) 为一个位于约束面且满足(x(0), y(0), z(0)) = P的参数化的曲线 最后 令 h(t) = f(x(t), y(t), z(t)),如上保证了 t=0时,h(t)取极大值
Taking a derivative using the chain rule in vector form gives
运用链式求导法则
h' (t) = ∇f| r(t) · r' (t).
//说明:f对r(t)求导✖r' (t)
Since t = 0 is a local maximum, we have h' (0) = ∇f| P · r' (0) = 0.
//说明:t=0时,h(t)取极大值,故h' (0)=0
Thus, ∇f| P is perpendicular to any curve on the constraint surface through P. This implies ∇f| P is perpendicular to the surface. Since ∇g| P is also perpendicular to the surface we have proved ∇f| P is parallel to ∇g| P .
因此,∇f| P (在P点处的∇f)垂直于在约束面上通过P点的任意曲线 即 ∇f| P 垂直于约束面 又因 ∇g| P 也垂直于约束面 得 ∇f| P // ∇g| P.
综上,可以进一步推断, 在受约束系统中,目标函数局部最大值和最小值(统称为极值)出现在临界点处.
利用 ∇f| P // ∇g| P,
我们可以构造辅助函数, L(x,y,λ)=f(x,y)+λ·g(x,y) (g(x,y)=c)
可知当 L(x,y,λ)取极值时,
因为 ∇L|P= ∇f| P + ∇g| P=k·∇f| P=0
目标函数 f(x,y)此时同样也取极值
QED
证明完毕
